ASE 笔记

得到晶胞参数(方法一：Numpy)

通过线性代数运算计算晶胞参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Numpy
from ase import Atoms
import numpy as np
from ase.io import read

atoms = read('POSCAR')
# 基矢
cell = atoms.cell
latticelength = np.dot(cell, cell.T).diagonal()
latticelength = latticelength ** 0.5

cos_alpha = np.dot(cell[1], cell[2]) / (latticelength[1] * latticelength[2])
cos_beta = np.dot(cell[0], cell[2]) / (latticelength[0] * latticelength[2])
cos_gamma = np.dot(cell[0], cell[1]) / (latticelength[0] * latticelength[1])

alpha = np.degrees(np.arccos(cos_alpha))
beta = np.degrees(np.arccos(cos_beta))
gamma = np.degrees(np.arccos(cos_gamma))

# 输出
print(latticelength[0],latticelength[1],latticelength[2],alpha, beta, gamma)

  1. 晶胞矩阵（Cell Matrix）：
    假设cell是一个 (3 \times 3) 的矩阵，表示晶胞的基矢量（a、b、c）：
    [
    \text{cell} = \begin{pmatrix}
    a_x & a_y & a_z \
    b_x & b_y & b_z \
    c_x & c_y & c_z \
    \end{pmatrix}
    ]
    这里，a、b、c是晶胞的基矢量，分别对应晶胞的三个边。

  2. 点乘计算内积：
    使用np.dot(cell, cell.T)计算基矢量的内积：
    [
    \text{cell} \cdot \text{cell}^T = \begin{pmatrix}
    a_x & a_y & a_z \
    b_x & b_y & b_z \
    c_x & c_y & c_z \
    \end{pmatrix} \cdot \begin{pmatrix}
    a_x & b_x & c_x \
    a_y & b_y & c_y \
    a_z & b_z & c_z \
    \end{pmatrix}
    ]
    得到的结果是一个对称矩阵：
    [
    \text{dot_product} = \begin{pmatrix}
    a \cdot a & a \cdot b & a \cdot c \
    b \cdot a & b \cdot b & b \cdot c \
    c \cdot a & c \cdot b & c \cdot c \
    \end{pmatrix}
    ]

  3. 提取对角线元素：
    使用.diagonal()提取对角线上的元素，这些元素分别是基矢量的内积：
    [
    \text{diagonal} = \begin{pmatrix}
    a \cdot a \
    b \cdot b \
    c \cdot c \
    \end{pmatrix}
    ]

  4. 计算晶胞长度：
    对对角线元素开平方，得到晶胞的基矢量的长度（即晶胞参数）：
    [
    \text{latticelength} = \begin{pmatrix}
    \sqrt{a \cdot a} \
    \sqrt{b \cdot b} \
    \sqrt{c \cdot c} \
    \end{pmatrix} = \begin{pmatrix}
    |a| \
    |b| \
    |c| \
    \end{pmatrix}
    ]

  5. 得到晶胞的角度（α, β, γ）
    晶胞的基矢量为：
    [
    \text{cell} = \begin{pmatrix}
    a_x & a_y & a_z \
    b_x & b_y & b_z \
    c_x & c_y & c_z \
    \end{pmatrix}
    ]
    晶胞的长度已经计算为：$a,b,c$

    晶胞的角度：

[ \cos(\alpha) = \frac{\mathbf{b} \cdot \mathbf{c}}{|b| \cdot |c|} ]
[ \cos(\beta) = \frac{\mathbf{a} \cdot \mathbf{c}}{|a| \cdot |c|} ]
[ \cos(\gamma) = \frac{\mathbf{a} \cdot \mathbf{b}}{|a| \cdot |b|} ]

得到晶胞参数(方法二：ASE)

1
2
3
4
5
6
7
8
# ASE
from ase import Atoms
from ase.io import read

atoms = read('POSCAR')
# atoms.cell.cellpar()方法
length_a, length_b, length_c, angle_bc, angle_ac, angle_ab = atoms.cell.cellpar()
print(length_a, length_b, length_c, angle_bc, angle_ac, angle_ab)

恒电势方法的理解

参考 J. Am. Chem. Soc. 2022, 144, 39, 18144–18152
何政达——b站，恒电势

  1. 公式1，改变电荷后的系统能量：
    [ E = E_{DFT}-\Delta n(V_{sol}+\Phi_q/e) ]
    $E_{DFT}$ 为 DFT 能量，e 为单位转化，Vsol 为体系的静电势，$\Phi_q$ 为体系相对于费米能级的功函数，$\Delta n$ 为电荷的变化量。
  2. 公式2，改变电荷后，系统的电势：
    [ U_q(V/SHE) = -4.6,V-\Phi_q/e ]
  3. 公式3，$E-U_q$的二次关系：
    [ E(U_q) = -\frac{1}{2}C(U_{q}-U_0)^2+E_0]
    $U_q$为电势，$U_0$为零电荷电势(PZC)，C为系统电容，$E_0$为PAC下的能量。

得到对应电势的能量值

1
2
3
4
5
6
7
# INCAR
TAU = 0
LAMBDA_D_K = 3
LVHAR = T
LSOL = T
IDIPOL = 3
NELECT = sum(POTCAR) ± ne
  1. ${\Delta n}$：改变的 INCAR 参数 NELECT (Δn)
  2. ${\Phi_q}$：从 OUTCAR 中读取费米能级 E_fermi; 从 LOCPOT 中读取 vtot
  3. ${E_0}$：get energy from OUTCAR
  4. SHE和RHE的转化
    J.Am.Chem. Soc. 2024, 146,14954−14958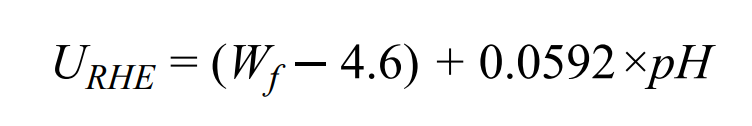
    SHE

电势校正
[E_{SHE} = E_{measured}+E_{reference}]
[E_{RHE} = E_{SHE}+0.0592pH ]