Notes of datastructure
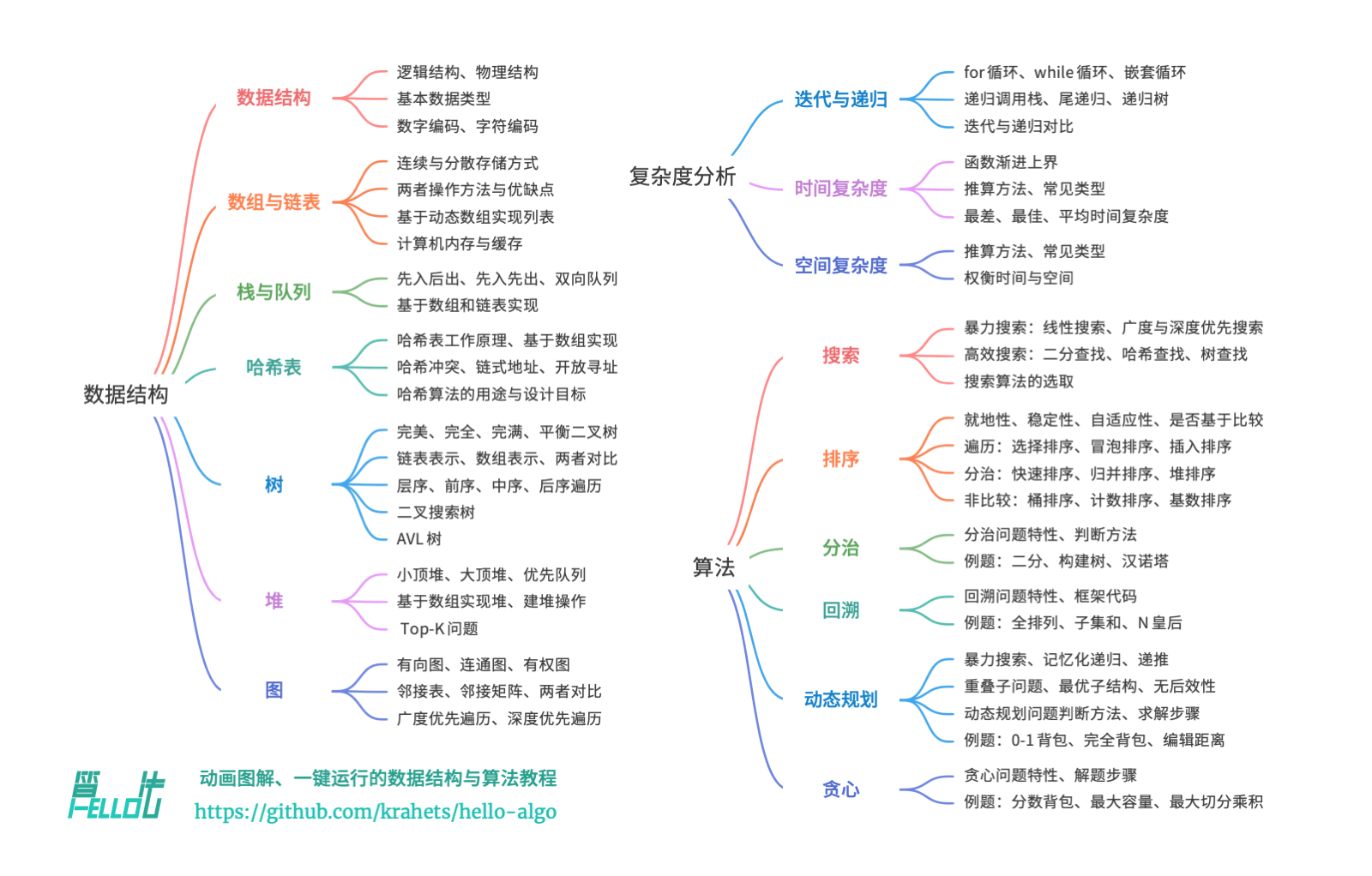
图片存放 images/001/
第一章:初识算法
算法(algorithm)数据结构(data structure)
- 生活中的二分法,排序,贪心算法:查字典,整理扑克,找零钱。
- 数据结构设计是一个充满权衡的过程。如果想在某方面取得提升,往往需要在另一方面作出妥协。
- 数据结构为算法提供了结构化存储的数据,以及操作数据的方法。
数据结构本身仅存储数据信息,结合算法才能解决特定问题。
算法通常可以基于不同的数据结构实现,但执行效率可能相差很大,选择合适的数据结构是关键。 - 在实际讨论时,我们通常会将“数据结构与算法”简称为“算法”。
第二章 复杂度分析
渐近复杂度分析(asymptotic complexity analysis)
时间复杂度(time complexity)
- 重复操作:迭代(iteration)递归(recursion)
- for 循环是最常见的迭代形式之一,适合在预先知道迭代次数时使用。while 循环比 for 循环的自由度更高。
- 每一次嵌套都是一次“升维”,将会使时间复杂度
- 迭代:“自下而上”地解决问题。从最基础的步骤开始,然后不断重复或累加这些步骤,直到任务完成。
- 递归:“自上而下”地解决问题。将原问题分解为更小的子问题,这些子问题和原问题具有相同的形式。接下来将子问题继续分解为更小的子问题,直到基本情况时停止(基本情况的解是已知的)。
- 递归通常比迭代更加耗费内存空间。因此递归通常比循环的时间效率更低。过深的递归可能导致栈溢出错误。适用于子问题分解,如树、图、分治、回溯等,代码结构简洁、清晰.
- O(n) 时间复杂度分析统计的不是算法运行时间,而是算法运行时间随着数据量变大时的增长趋势。
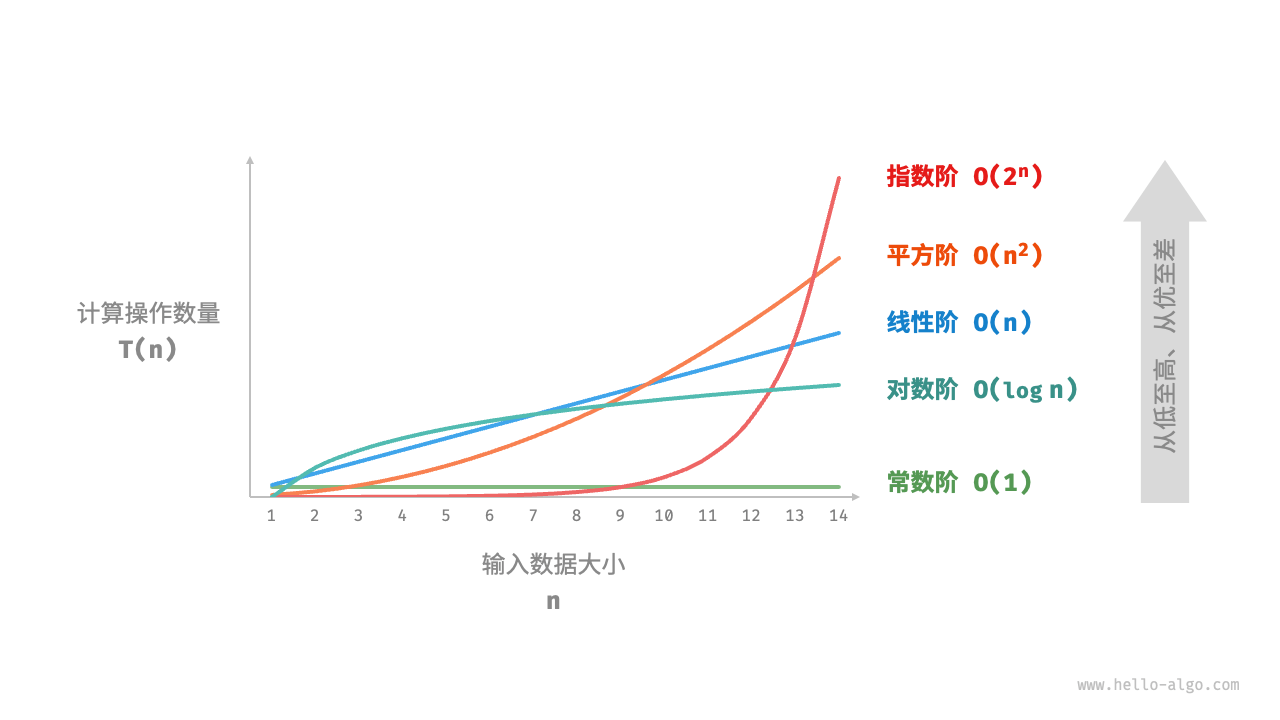
- 指数阶增长非常迅速,在穷举法(暴力搜索、回溯等)中比较常见。对于数据规模较大的问题,指数阶是不可接受的,阶乘阶比指数阶增长得更快.通常需要使用动态规划或贪心算法等来解决。对数阶常出现于基于分治策略的算法中,体现了“一分为多”和“化繁为简”的算法思想。它增长缓慢,是仅次于常数阶的理想的时间复杂度。主流排序算法的时间复杂度通常为 O(nlogn) ,例如快速排序、归并排序、堆排序等。
空间复杂度(space complexity)
- 一般情况下,空间复杂度的统计范围是“暂存空间”加上“输出空间”
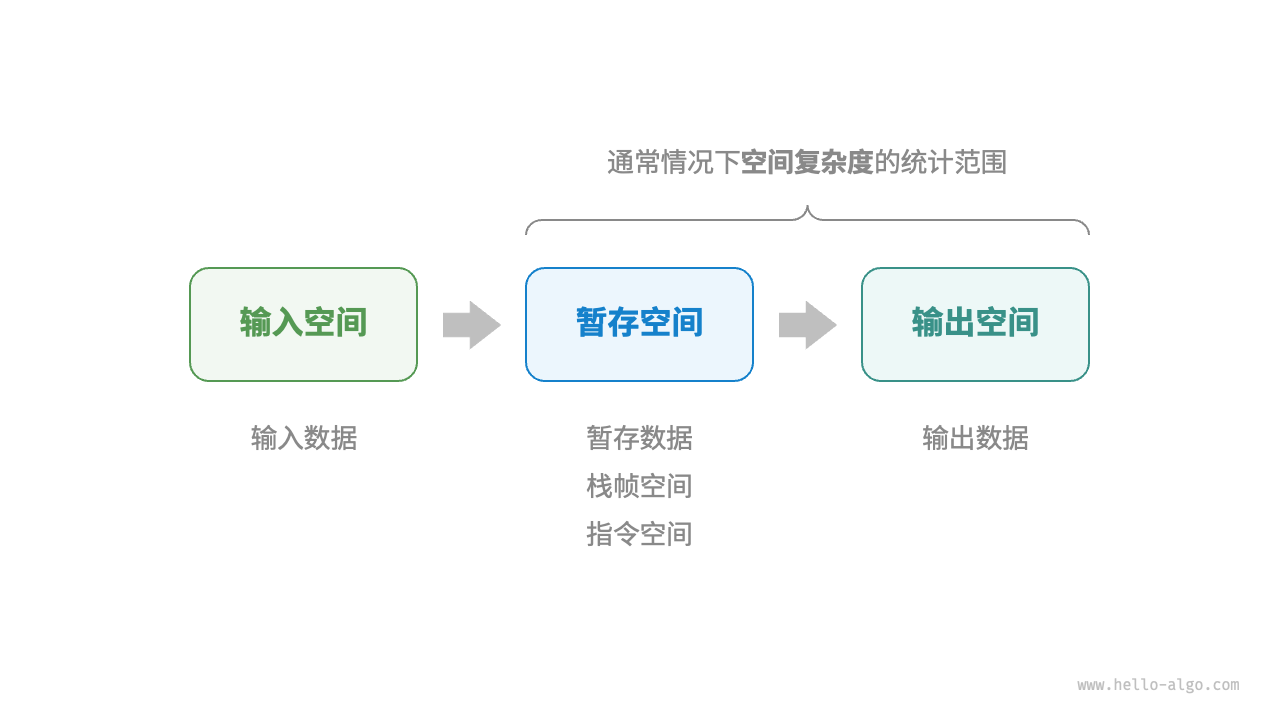
hmap = dict[int, str]()这一行代码的意思是创建一个类型为 dict[int, str] 的空字典- 降低时间复杂度通常需要以提升空间复杂度为代价,反之亦然。我们将牺牲内存空间来提升算法运行速度的思路称为“以空间换时间”;反之,则称为“以时间换空间”。
- 函数(function)可以被独立执行,所有参数都以显式传递。方法(method)与一个对象关联,被隐式传递给调用它的对象,能够对类的实例中包含的数据进行操作。C 语言是过程式编程语言,没有面向对象的概念,所以只有函数。C++ 和 Python 既支持过程式编程(函数),也支持面向对象编程(方法)。
第三章 数据结构
3.1 数据结构
内存资源
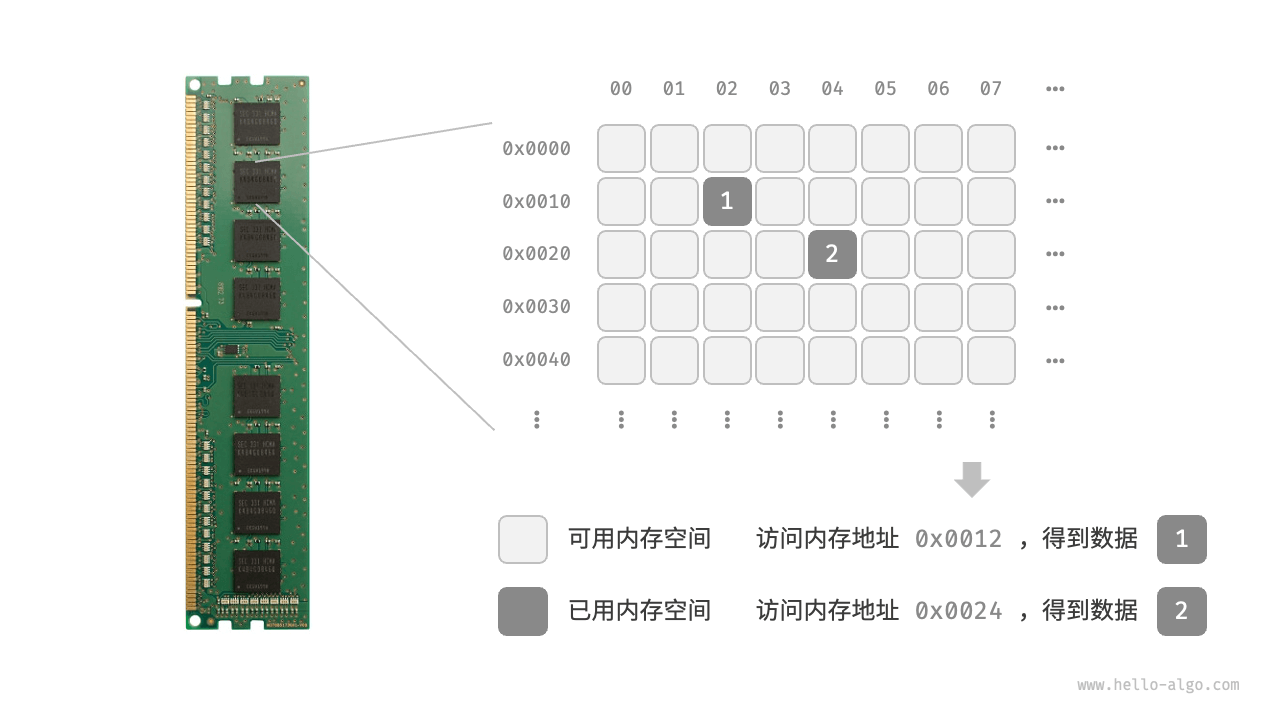
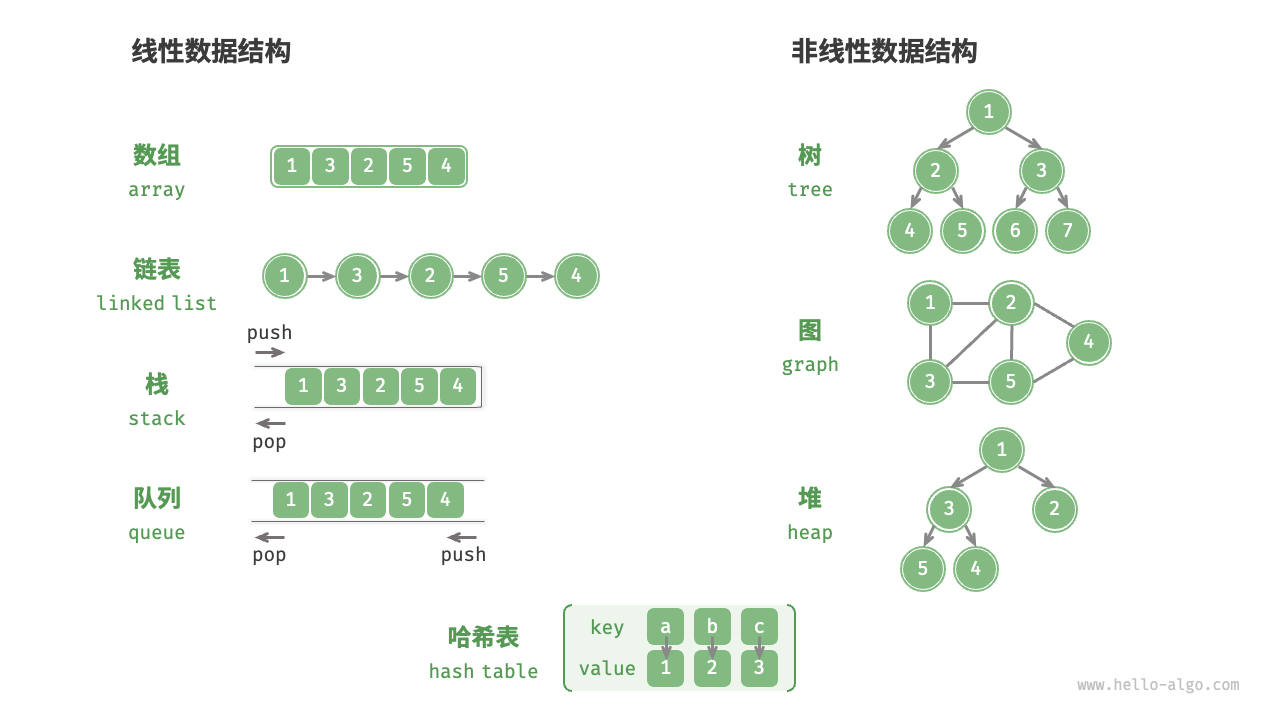
- 物理结构反映了数据在计算机内存中的存储方式,可分为连续空间存储(数组)和分散空间存储(链表)
-
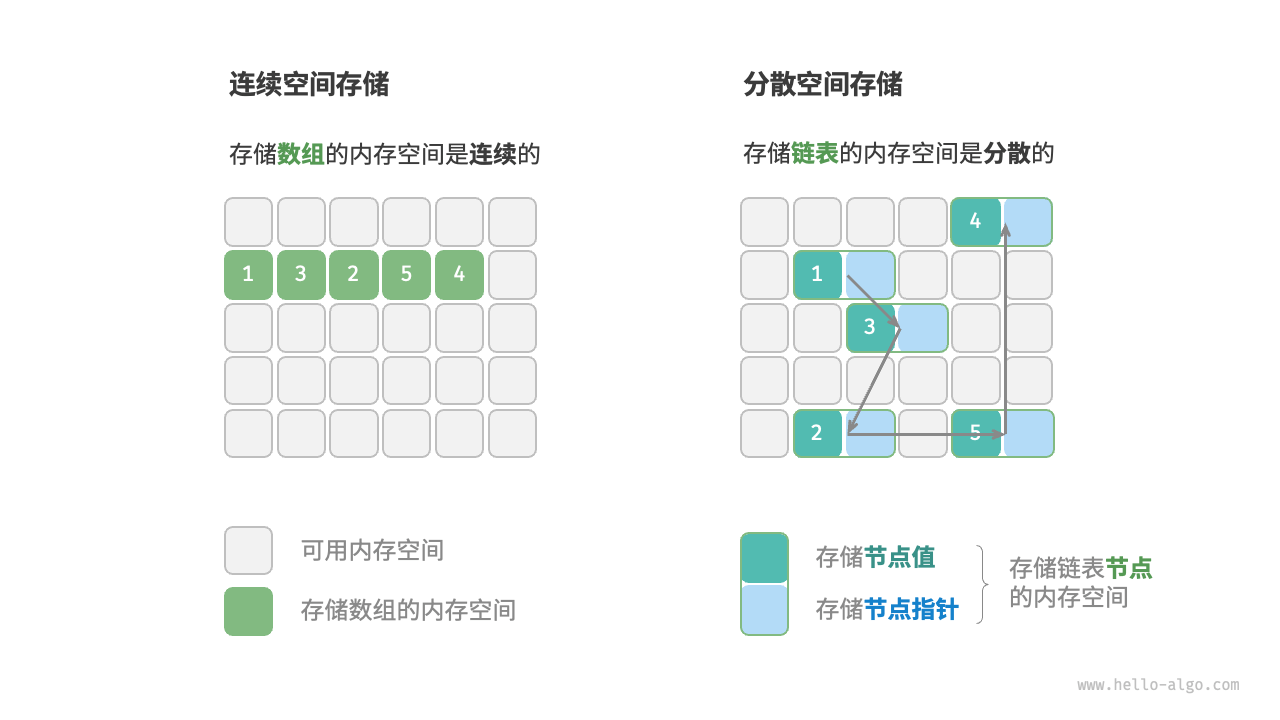
- 所有数据结构都是基于数组、链表或二者的组合实现的。基于数组可实现:栈、队列、哈希表、树、堆、图、矩阵、张量(维度
的数组)等。
基于链表可实现:栈、队列、哈希表、树、堆、图等。 - 链表在初始化后,仍可以在程序运行过程中对其长度进行调整,因此也称“动态数据结构”。数组在初始化后长度不可变,因此也称“静态数据结构”。值得注意的是,数组可通过重新分配内存实现长度变化,从而具备一定的“动态性”。
3.2 基本数据类型
- 基本数据类型是 CPU 可以直接进行运算的类型,在算法中直接被使用,主要包括以下几种。
整数类型 byte、short、int、long 。
浮点数类型 float、double ,用于表示小数。
字符类型 char ,用于表示各种语言的字母、标点符号甚至表情符号等。
布尔类型 bool ,用于表示“是”与“否”判断。 - 基本数据类型以二进制的形式存储在计算机中。一个二进制位即为1比特。在绝大多数现代操作系统中,1字节(byte)由8比特(bit)组成。
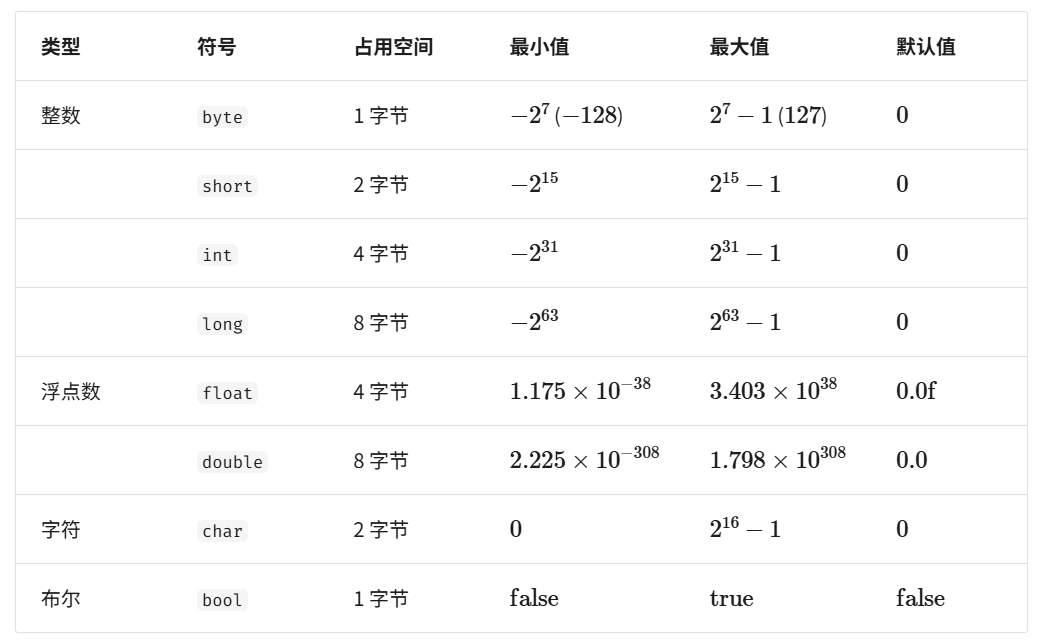
在 Python 中,整数类型 int 可以是任意大小,只受限于可用内存;浮点数 float 是双精度 64 位;没有 char 类型,单个字符实际上是长度为 1 的字符串 str 。字符 char 的大小在 C 和 C++ 中为 1 字节,即使表示布尔量仅需 1 位,0/1,它在内存中通常也存储为 1 字节。这是因为现代计算机 CPU 通常将 1 字节作为最小寻址内存单元。 - 基本数据类型提供了数据的“内容类型”,而数据结构提供了数据的“组织方式”。
3.3 数字编码*
3.4 字符编码*
第四章 数组与链表
4.1 数组
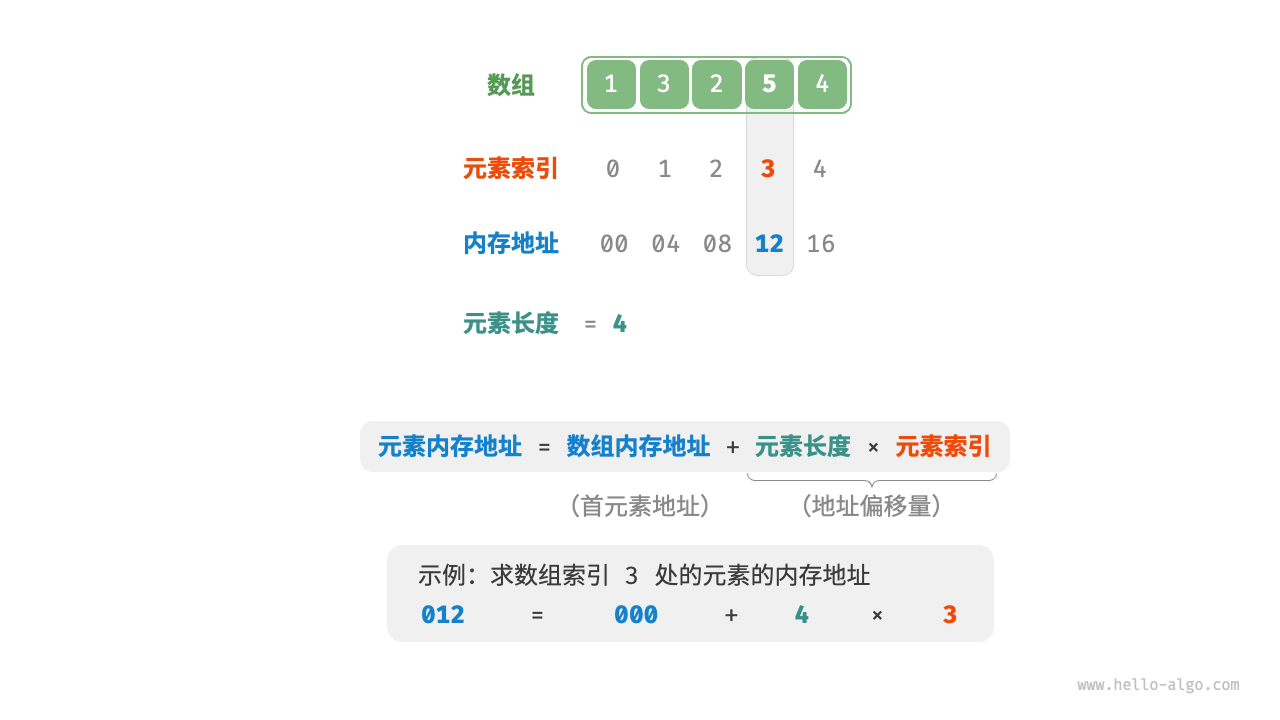
- 数组的索引本质上是内存地址的偏移量。
- 空间效率高:数组为数据分配了连续的内存块,无须额外的结构开销。插入与删除效率低:当数组中元素较多时,插入与删除操作需要移动大量的元素。
- 支持随机访问:数组允许在O(1)时间内访问任何元素。长度不可变:数组在初始化后长度就固定了,扩容数组需要将所有数据复制到新数组,开销很大。
- 缓存局部性:当访问数组元素时,计算机不仅会加载它,还会缓存其周围的其他数据,从而借助高速缓存来提升后续操作的执行速度。空间浪费:如果数组分配的大小超过实际所需,那么多余的空间就被浪费了。
4.2 链表
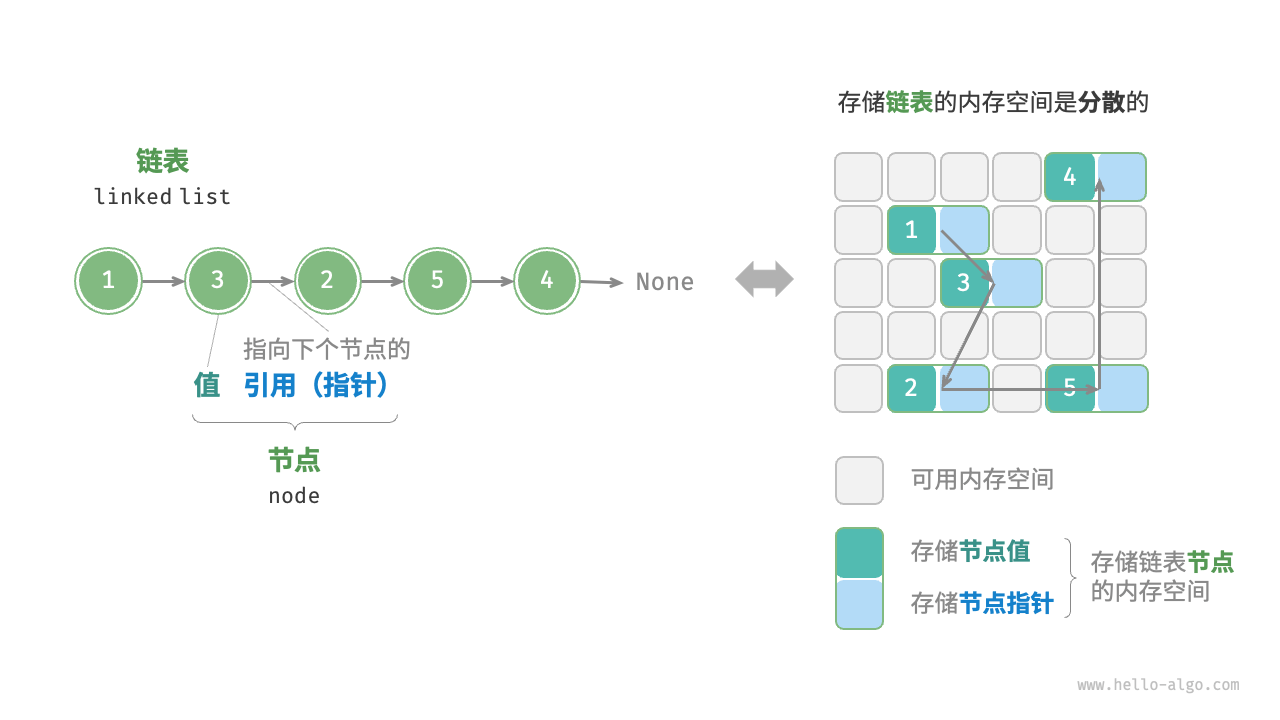
- 链表节点 ListNode 除了包含值,还需额外保存一个引用(指针)。因此在相同数据量下,链表比数组占用更多的内存空间。
- 单向链表通常用于实现栈、队列、哈希表和图等数据结构。
栈与队列:当插入和删除操作都在链表的一端进行时,它表现的特性为先进后出,对应栈;当插入操作在链表的一端进行,删除操作在链表的另一端进行,它表现的特性为先进先出,对应队列。
哈希表:链式地址是解决哈希冲突的主流方案之一,在该方案中,所有冲突的元素都会被放到一个链表中。
图:邻接表是表示图的一种常用方式,其中图的每个顶点都与一个链表相关联,链表中的每个元素都代表与该顶点相连的其他顶点。 - 双向链表:快速查找前一个和后一个元素
高级数据结构:比如在红黑树、B 树中,我们需要访问节点的父节点,这可以通过在节点中保存一个指向父节点的引用来实现,类似于双向链表。
浏览器历史:在网页浏览器中,当用户点击前进或后退按钮时,浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。
LRU 算法:在缓存淘汰(LRU)算法中,我们需要快速找到最近最少使用的数据,以及支持快速添加和删除节点。这时候使用双向链表就非常合适。 - 环形链表常用于需要周期性操作的场景,比如操作系统的资源调度。
4.3 列表
列表(list)是一个抽象的数据结构概念,它表示元素的有序集合,支持元素访问、修改、添加、删除和遍历等操作,无须使用者考虑容量限制的问题。列表可以基于链表或数组实现。
- 当使用数组实现列表时,长度不可变的性质会导致列表的实用性降低。我们可以使用动态数组(dynamic array)来实现列表。
- 许多编程语言中的标准库提供的列表是基于动态数组实现的, Python 中的 list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23# 初始化列表
nums: list[int] = [1, 3, 2, 5, 4]
# 清空列表
nums.clear()
# 尾部添加元素1
nums.append(1)
# 在中间插入元素,在索引3处插入数字6
nums.insert(3, 6)
# 删除元素
nums.pop(3)
# 通过索引遍历列表
count = 0
for i in range(len(nums)):
count += nums[i]
# 直接遍历列表元素
for num in nums:
count += num
# 拼接两个列表
nums1: list[int] = [6, 8, 7, 10, 9]
nums += nums1 # 将列表 nums1 拼接到 nums 之后
# 排序列表
nums.sort() # 排序后,列表元素从小到大排列 - 列表实现:https://www.hello-algo.com/chapter_array_and_linkedlist/list/#432
4.3 内存与缓存
计算机中包括三种类型的存储设备:硬盘(hard disk)、内存(random-access memory, RAM)、缓存(cache memory)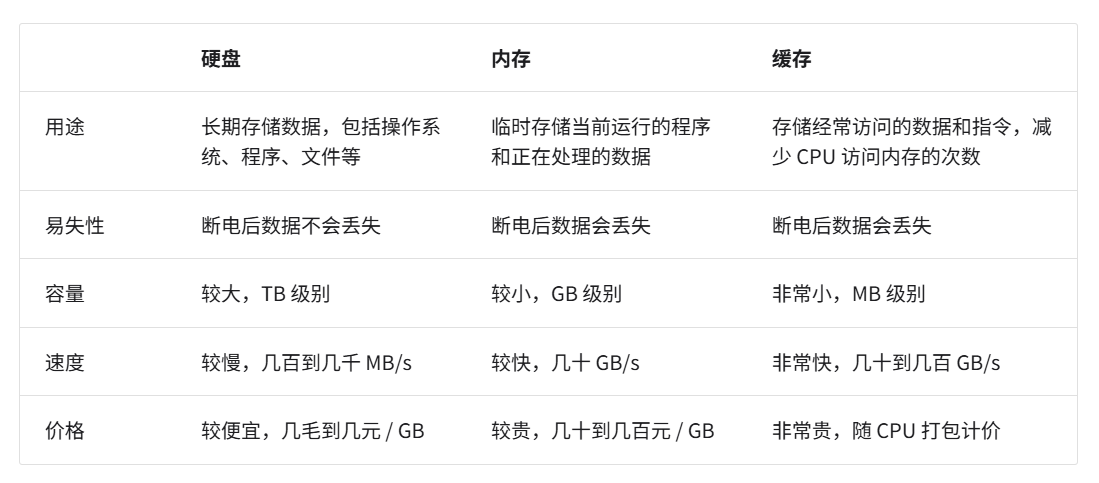
- 硬盘用于长期存储大量数据,内存用于临时存储程序运行中正在处理的数据,而缓存则用于存储经常访问的数据和指令,以提高程序运行效率。三者共同协作,确保计算机系统高效运行。
- 在程序运行时,数据会从硬盘中被读取到内存中,供 CPU 计算使用。缓存可以看作 CPU 的一部分,它通过智能地从内存加载数据,给 CPU 提供高速的数据读取,从而显著提升程序的执行效率,减少对较慢的内存的依赖。
第五章 栈与队列
5.1 栈
栈(stack):先入后出;类比为叠猫猫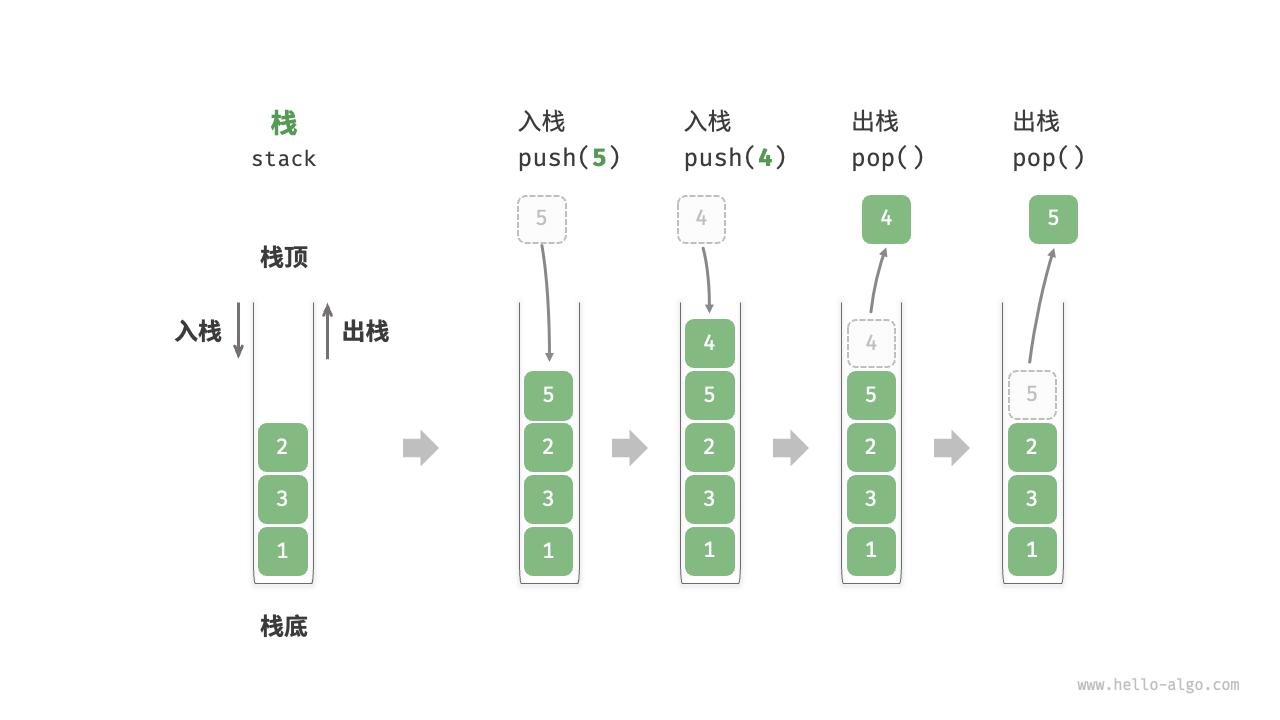
- Python 没有内置的栈类
- 只能在栈顶添加或删除元素,因此栈可以视为一种受限制的数组或链表
<基于链表和数组实现的栈.ipynb> - 在基于数组的实现中,入栈和出栈操作都在预先分配好的连续内存中进行,具有很好的缓存本地性,因此效率较高。然而,如果入栈时超出数组容量,会触发扩容机制,导致该次入栈操作的时间复杂度变为O(n)。
- 在基于链表的实现中,链表的扩容非常灵活,不存在上述数组扩容时效率降低的问题。但是,入栈操作需要初始化节点对象并修改指针,因此效率相对较低。不过,如果入栈元素本身就是节点对象,那么可以省去初始化步骤,从而提高效率。基于链表实现的栈可以提供更加稳定的效率表现。
- 在初始化列表时,系统会为列表分配“初始容量”,该容量可能超出实际需求;并且,扩容机制通常是按照特定倍率(例如 2 倍)进行扩容的,扩容后的容量也可能超出实际需求。因此,基于数组实现的栈可能造成一定的空间浪费。然而,由于链表节点需要额外存储指针,因此链表节点占用的空间相对较大。
- 浏览器中的后退与前进、软件中的撤销与反撤销。程序内存管理。每次调用函数时,系统都会在栈顶添加一个栈帧,用于记录函数的上下文信息。
5.2 队列
队列(queue)先入先出;猫猫排队
<基于链表和数组实现的队列.ipynb>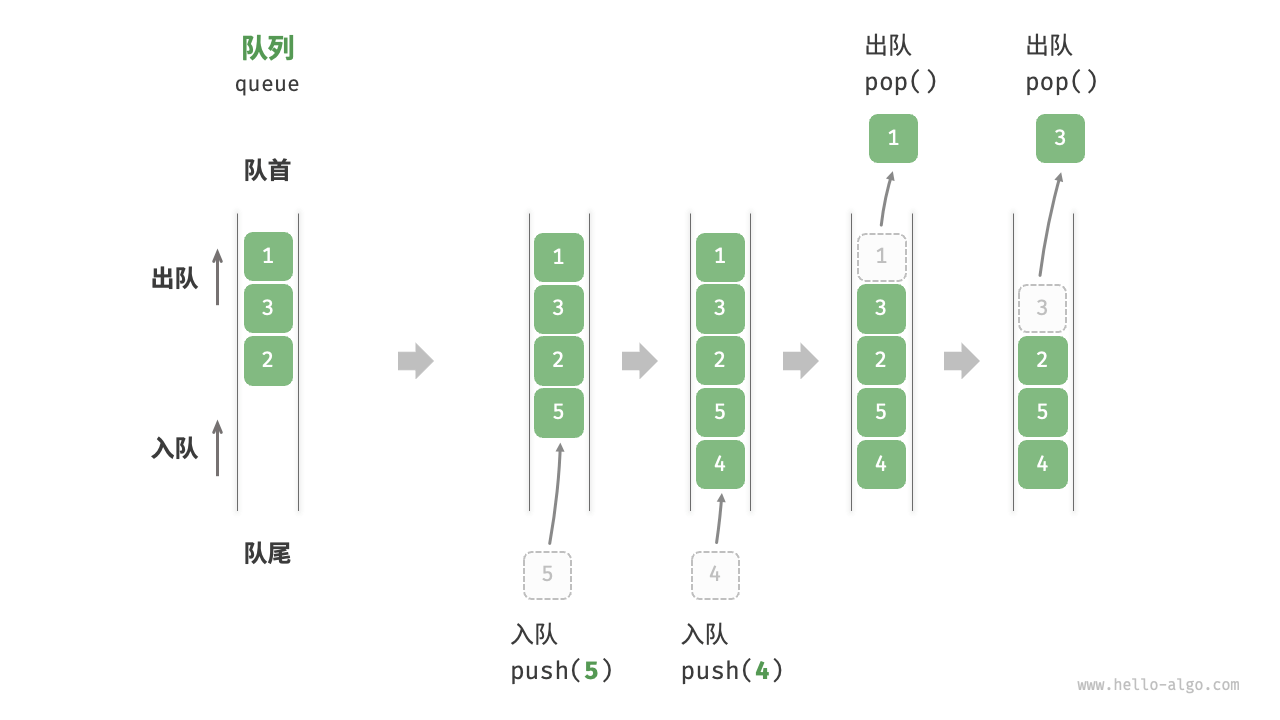
- 淘宝订单。购物者下单后,订单将加入队列中,系统随后会根据顺序处理队列中的订单。在双十一期间,短时间内会产生海量订单,高并发成为工程师们需要重点攻克的问题。
- 各类待办事项。任何需要实现“先来后到”功能的场景,例如打印机的任务队列、餐厅的出餐队列等,队列在这些场景中可以有效地维护处理顺序。
- 在队列中,我们仅能删除头部元素或在尾部添加元素。如图 5-7 所示,双向队列(double-ended queue)提供了更高的灵活性,允许在头部和尾部执行元素的添加或删除操作。
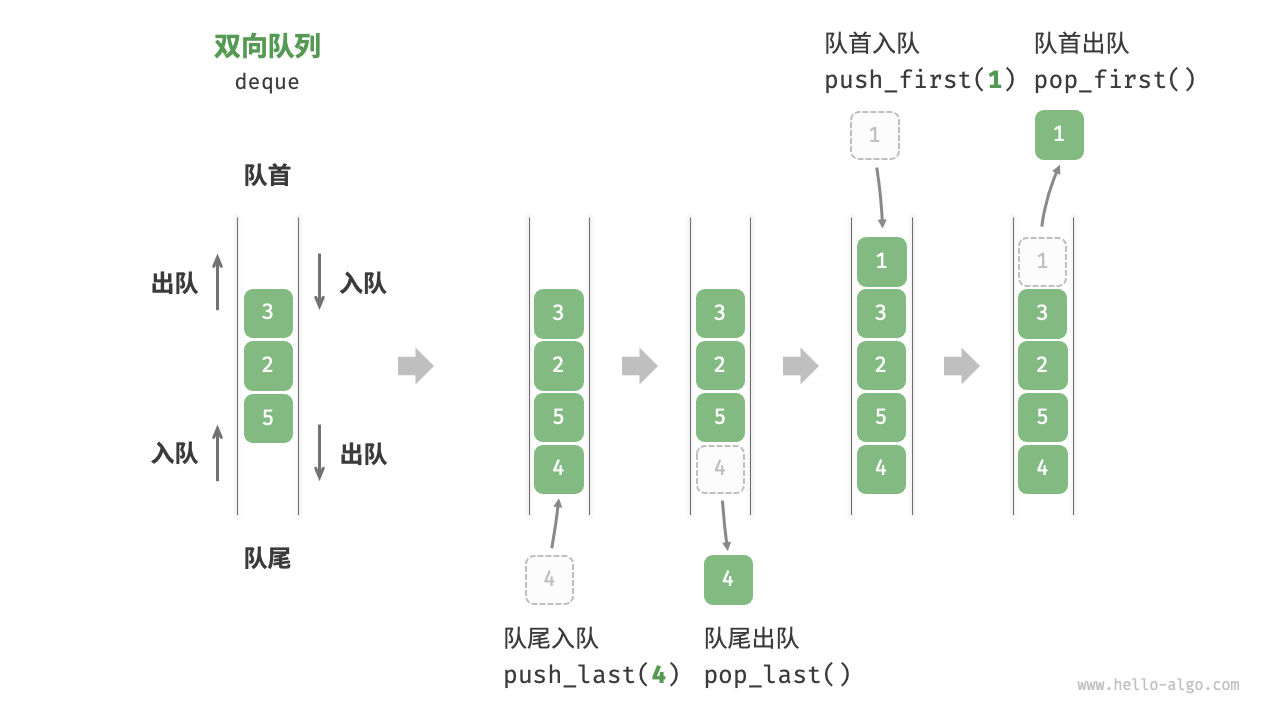
- 双向队列兼具栈与队列的逻辑,因此它可以实现这两者的所有应用场景,同时提供更高的自由度。
- 软件的“撤销”功能通常使用栈来实现:系统将每次更改操作 push 到栈中,然后通过 pop 实现撤销。然而,考虑到系统资源的限制,软件通常会限制撤销的步数。当栈的长度超过时,软件需要在栈底(队首)执行删除操作。但栈无法实现该功能,此时就需要使用双向队列来替代栈。“撤销”的核心逻辑仍然遵循栈的先入后出原则,只是双向队列能够更加灵活地实现一些额外逻辑。
6. 使用两个栈,栈 A 用于撤销,栈 B 用于反撤销。
每当用户执行一个操作,将这个操作压入栈 A ,并清空栈 B 。
当用户执行“撤销”时,从栈 A 中弹出最近的操作,并将其压入栈 B 。
当用户执行“反撤销”时,从栈 B 中弹出最近的操作,并将其压入栈 A 。
第六章 哈希表
哈希表(hash table),又称散列表。它通过建立键 key 与值 value 之间的映射,实现高效的元素查询。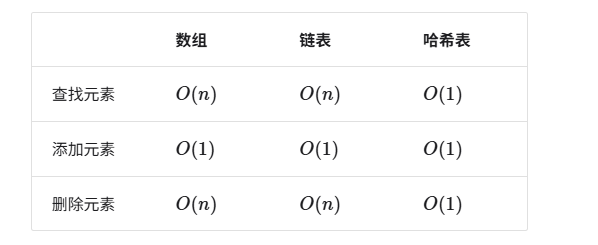
在哈希表中进行增删查改的时间复杂度都是O(1),非常高效。
常用操作
增删查改
1 | # 初始化哈希表 |
遍历操作
1 | # 遍历键值对 key->value |
<哈希表的简单实现.ipynb>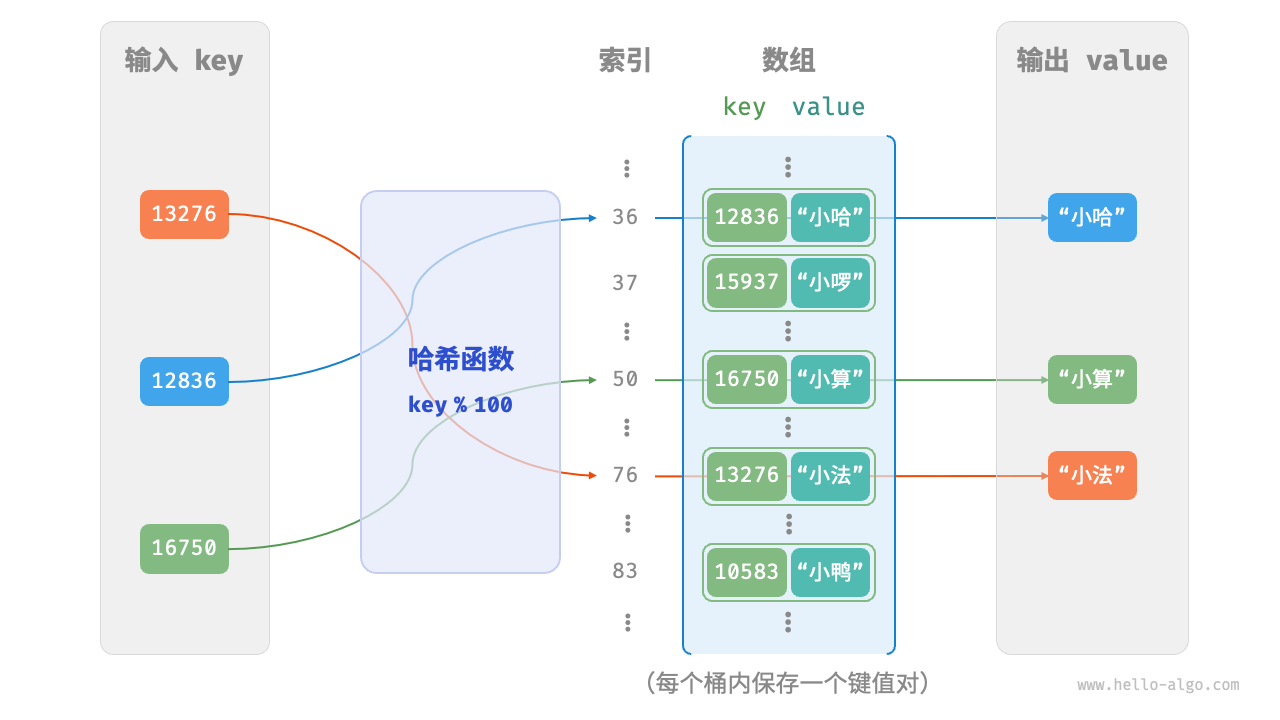
哈希冲突*
- 通常情况下哈希函数的输入空间远大于输出空间,因此理论上哈希冲突是不可避免的。比如,输入空间为全体整数,输出空间为数组容量大小,则必然有多个整数映射至同一桶索引。
- 哈希表容量n越大,多个 key 被分配到同一个桶中的概率就越低,冲突就越少。因此,我们可以通过扩容哈希表来减少哈希冲突。
- 类似于数组扩容,哈希表扩容需将所有键值对从原哈希表迁移至新哈希表,非常耗时;并且由于哈希表容量 capacity 改变,我们需要通过哈希函数来重新计算所有键值对的存储位置,这进一步增加了扩容过程的计算开销。为此,编程语言通常会预留足够大的哈希表容量,防止频繁扩容。
- 负载因子(load factor)是哈希表的元素数量除以桶数量,用于衡量哈希冲突的严重程度。
- 改良哈希表数据结构,使得哈希表可以在出现哈希冲突时正常工作。仅在必要时,即当哈希冲突比较严重时,才执行扩容操作。哈希表的结构改良方法主要包括“链式地址”和“开放寻址”。
哈希算法
二叉树
二叉树(binary tree)是一种非线性数据结构。
二叉树的基本单元是节点,每个节点包含值、左子节点引用和右子节点引用。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 初夏阳光!
